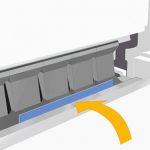
1. బెండింగ్ ప్రక్రియను అర్థం చేసుకోవడం: సాధారణ వాస్తవాలు
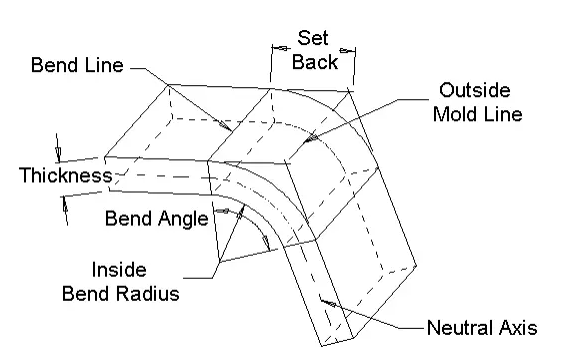
బెండ్ అలవెన్స్ = యాంగిల్ * (T/ 180)*(వ్యాసార్థం + K-కారకం *మందం) బెండ్ కాంపెన్సేషన్ = బెండ్ అలవెన్స్-(2 * సెట్ బ్యాక్)
లోపల సెట్ బ్యాక్ = టాన్ (యాంగిల్ / 2) *రేడియస్ అవుట్సైడ్సెట్ బ్యాక్ = టాన్ (యాంగిల్ / 2)*(వ్యాసార్థం + మందం)

1) వంగిన భాగంలో పొందిన వ్యాసార్థం మనం ఆ భాగాన్ని (వంగడానికి ముందు) కత్తిరించాల్సిన పొడవును ప్రభావితం చేస్తుంది.
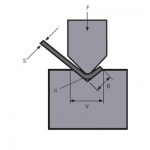
2) బెండింగ్లో పొందిన వ్యాసార్థం మనం పని చేయడానికి ఎంచుకున్న V ఓపెనింగ్పై 99% ఆధారపడి ఉంటుంది.
భాగాన్ని డిజైన్ చేయడానికి ముందు మరియు ఖచ్చితంగా ఖాళీలను కత్తిరించడం ప్రారంభించే ముందు, ప్రెస్ బ్రేక్పై భాగాన్ని వంచడానికి మనం ఏ V ఓపెనింగ్ ఉపయోగిస్తామో ఖచ్చితంగా తెలుసుకోవాలి.
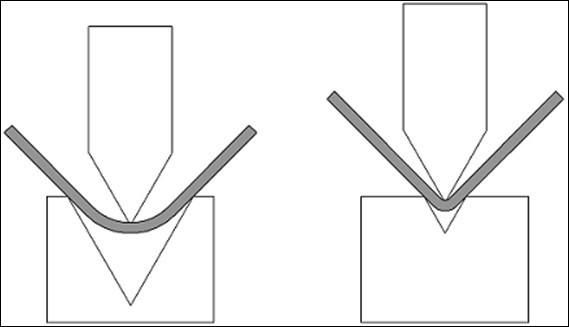
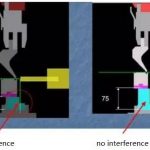
2. వ్యాసార్థం ఖాళీలను ఎలా ప్రభావితం చేస్తుంది
ఒక పెద్ద వ్యాసార్థం మన భాగం యొక్క కాళ్ళను బయటి వైపుకు "నెట్టు" చేస్తుంది, ఇది ఖాళీని "చాలా పొడవుగా" కత్తిరించినట్లు అభిప్రాయాన్ని ఇస్తుంది.
ఒక చిన్న వ్యాసార్థానికి ఖాళీ అవసరం ఉంటుంది, అది వ్యాసార్థం పెద్దదిగా ఉంటే దాని కంటే "కొంచెం పొడవు" కట్ చేయాలి.
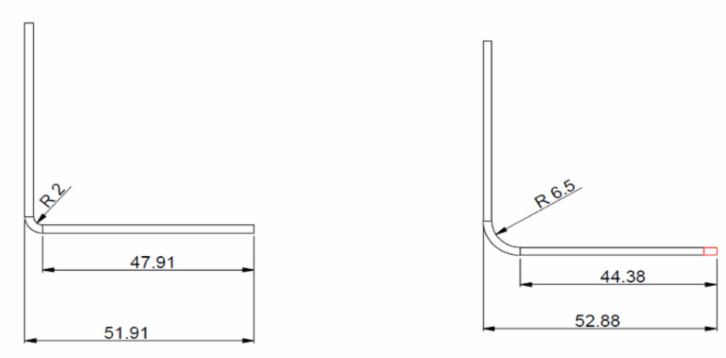
3. బెండింగ్ అలవెన్స్
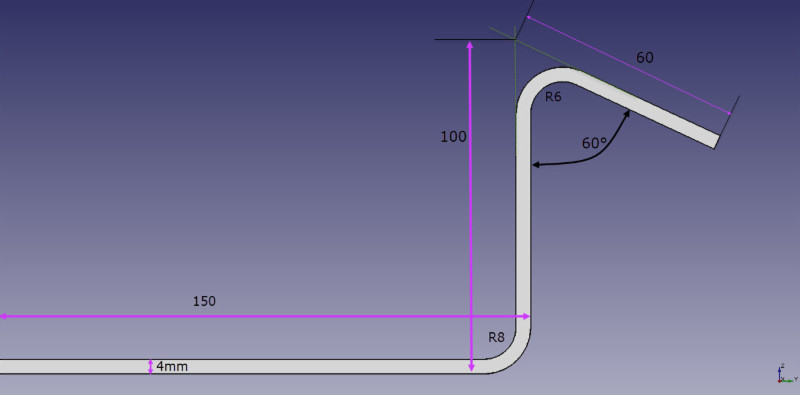
పై బొమ్మ యొక్క విప్పబడిన ఖాళీలు ఈ క్రింది విధంగా లెక్కించబడతాయి:
B = 150 + 100 + 60 + BA1 + BA2
BA1 మరియు BA2లను ఎలా లెక్కించాలి:
బెండింగ్ భత్యాన్ని గణిస్తోంది
ఫ్లాట్గా మారడం ద్వారా ఒకసారి అతివ్యాప్తి చెందడం ద్వారా రెండు కాళ్ల నుండి మనం తగ్గించాల్సిన భాగాన్ని మనం సాధారణంగా “బెండ్ అలవెన్స్” (లేదా సమీకరణంలో BA) అని పిలుస్తారు.
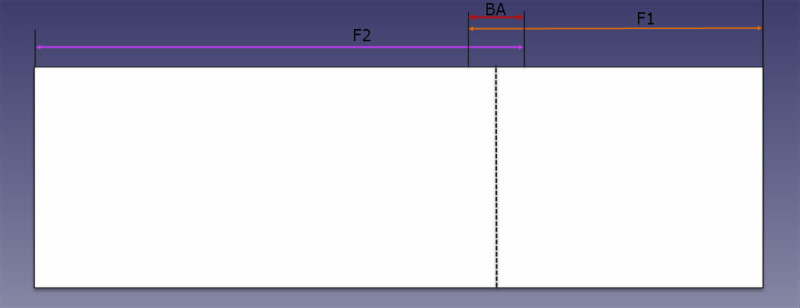
బెండింగ్ భత్యం సూత్రం
90° వరకు బెండ్ల కోసం BA ఫార్ములా
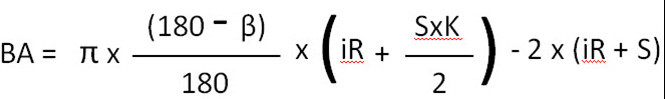
91° నుండి 165° వరకు వంపుల కోసం BA సూత్రం
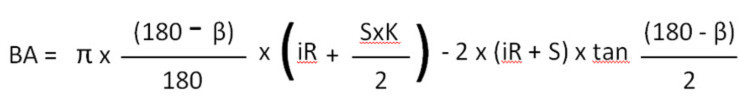
iR= అంతర్గత వ్యాసార్థం
S= మందం
Β = కోణం
Π = 3,14159265….
K = K కారకం
K కారకం
ప్రెస్ బ్రేక్పై వంగినప్పుడు షీట్ మెటల్ లోపలి భాగం కుదించబడుతుంది, అయితే బయటి భాగం విస్తరించబడుతుంది.
ఫైబర్లు కుదించబడని లేదా పొడిగించబడని షీట్లో కొంత భాగం ఉందని దీని అర్థం. మేము ఈ భాగాన్ని "తటస్థ అక్షం" అని పిలుస్తాము.
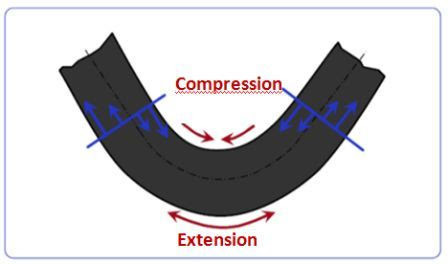
బెండ్ లోపలి నుండి తటస్థ అక్షం వరకు ఉన్న దూరాన్ని మనం K కారకం అని పిలుస్తాము.
ఈ విలువ మనం కొనుగోలు చేసే మెటీరియల్తో వస్తుంది మరియు దానిని మార్చడం సాధ్యం కాదు.
ఈ విలువ భిన్నాలలో వ్యక్తీకరించబడింది. K కారకం ఎంత చిన్నదైతే, తటస్థ అక్షం షీట్ లోపలి వ్యాసార్థానికి దగ్గరగా ఉంటుంది.
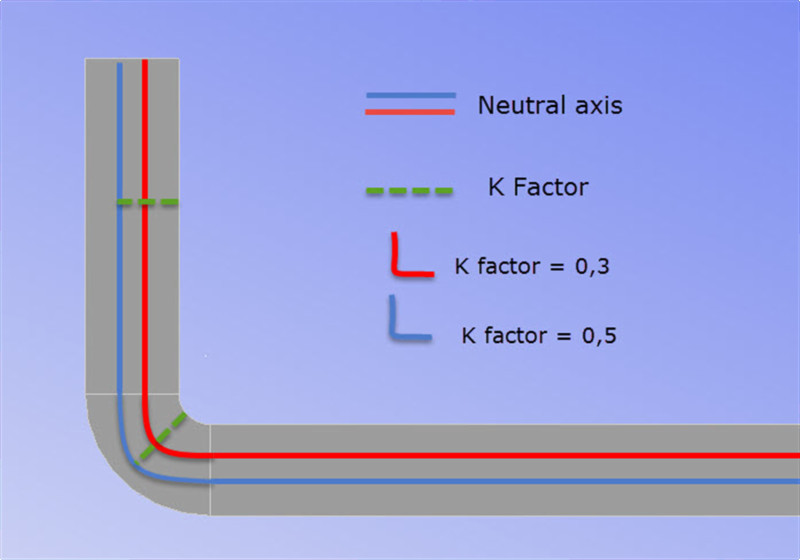
K కారకం = చక్కటి ట్యూనింగ్
K కారకం మా విప్పబడిన ఖాళీని ప్రభావితం చేస్తుంది. భాగం యొక్క వ్యాసార్థం అంత కాదు, కానీ ఖాళీల కోసం చక్కటి ట్యూనింగ్ గణనలుగా మనం భావించవచ్చు.
K కారకం ఎంత చిన్నదైతే, ఎక్కువ పదార్థం విస్తరించబడుతుంది మరియు అందువల్ల “బయటకు నెట్టబడుతుంది”…. అంటే మన కాలు "పెద్దది" అవుతుంది.
K కారకాన్ని అంచనా వేస్తోంది
చాలా సమయాలలో మన ఖాళీ గణనలను చక్కగా ట్యూన్ చేసేటప్పుడు K కారకాన్ని అంచనా వేయవచ్చు మరియు సర్దుబాటు చేయవచ్చు.
మనం చేయవలసిందల్లా కొన్ని పరీక్షలు (ఎంచుకున్న V ఓపెనింగ్లో) మరియు భాగం యొక్క వ్యాసార్థాన్ని కొలవడం.
మీరు మరింత ఖచ్చితమైన K కారకాన్ని గుర్తించాల్సిన అవసరం ఉన్నట్లయితే, మీ వంపు కోసం ఖచ్చితమైన K కారకాన్ని నిర్ణయించడానికి దిగువన గణన ఉంది.

K కారకం: ఒక సూత్రం
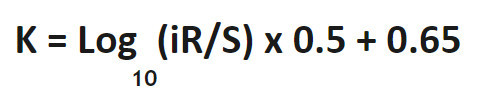
ఉదాహరణను పరిష్కరించడం:
B = 150 + 100 + 60 +BA1 + BA2
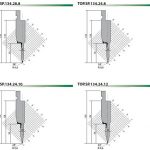
K కారకం అంచనా
B1: R/S=2 => K=0,8
B2: R/S=1,5 => K=0,8
రెండు వంపులు 90° లేదా అంతకంటే తక్కువ:
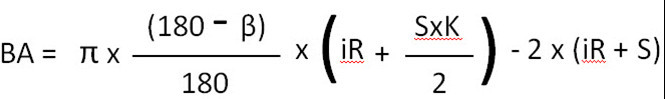
ఏమిటంటే:
B1 = 3.14 x 0.66 x (6 + ((4×0.8)/2) – 2 x 10
B1 = -4.25
B2 = 3.14 x 0.5 x (8 + ((4×0.8)/2) – 2 x 12
B2 = -8.93
అందువలన:
B = 150 + 100 + 60 + (-4.25) + (-8.93)
B= 296.8mm